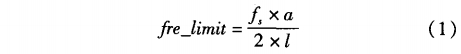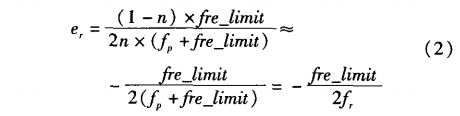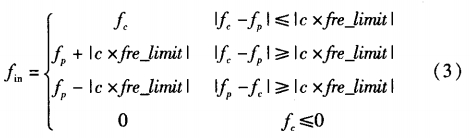摘要:對基于譜分析的數字式渦街流量計在應用中響應速度比較慢及其在小流量或小口徑時流量計輸出波動兩個問題進行了深入分析。采用設置門限值的方法提高了系統響應速度。對頻譜分析結果進行多次為0判斷,解決了系統輸出斷續問題。通過對頻譜分析結果的限幅,在平均時去掉超過標準差的頻率值,并去掉最大值和最小值,對平均結果進行第二次平均的方法減小了系統輸出的波動,提高了流量計輸出穩定性。
0引言
渦街流量計具有無可動部件維護方便、壓力損失小和輸出頻率量等優點,可以測量液體、氣體和蒸汽流量,應用相當廣泛。目前,渦街流量計主要有兩種處理方式,即脈沖整形計數方式和數字信號處理方式。其中,數字信號處理方式具有抗干擾能力強、量程比較寬和精度高的優點。基于譜分析的渦街流量計數字信號處理方法,采用DSP(數字信號處理器)芯片研制了實時處理系統,通過標定并應用于工業現場,取得了很好的效果。在應用中,針對數字式渦街流量計響應速度慢以及在小流量或者小口徑時輸出信號波動問題,進行了深人的分析,并提出了有效的解決方案。
1提高信號響應的速度
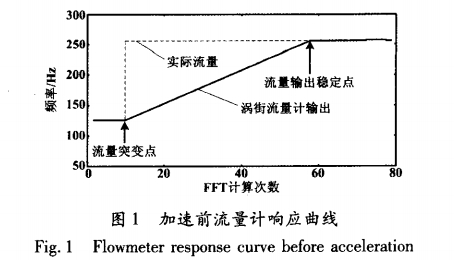
采用頻譜估計方法分析渦街信號的頻率是基于渦街流量計信號是一個平穩隨機過程信號,并且流量在短時間內是穩定的或變化很小。由于渦街流量計輸出信號實時性的要求,只能對有限長時間段內的信號進.行處理,即只能截取一段數據進行頻譜分析。為了防止數據統計變異性對計算渦街頻率的影響,必須對若干次頻譜分析的結果進行平均,這就需要花費時間。當平均次數多時,數字渦街流量計的響應速度就會顯得比較慢。例如,我們的系統采用時鐘頻率為40MHz的TMS320LF2407ADSP芯片,使用匯編語言編制FFT程序計算渦街信號的頻譜,對50次計算結果進行平均。每次FFT計算時間大概是300ms(包括信號處理,人機接口等對應的其他軟件執行時間),總用時大概為15s,這個時間比較長。若在這段時間里,流量發生突然變化,系統就需要計算50次FFT,才能反映流量的變化,這將造成測量誤差,如圖1所示。
在實際處理中,將每次頻譜分析后得到的渦街頻率放人一個循環隊列中,該隊列稱為隊列Q1,如圖2所示(數字表示隊列成員序號)。其中,最右邊的為隊首Q1,最左邊的為隊尾Q1。再按先進先出的原則對隊列中最新的若干個值進行平均,得到渦街輸出頻率。由于對隊列中的值不加判斷而直接參與平.均,導致系統響應速度變慢。
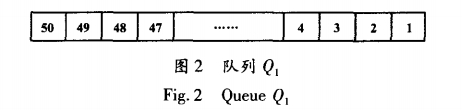
為此,通過設置門限值的方法來解決這個問題。根據隊列Q1中保存的過去的流量信息來設置一個頻率突變門限frelimit,如果連續計算出N個頻率值Q1[N]~Q1[1]都超過了fre._limit,則對這N個頻率值和后面進人隊列的值進行平均,而前面的值Q1[N+1]~Q1[50]不參加平均,N一般為3~5。理論上,門限fre_limit的選擇越小對微小突變就越敏感。但是,由于FFT計算出來的頻率會在--定范圍內波動,所以,門限值不能選擇太小。另外,由于小的突變造成的誤差不會太大,所以也沒必要將門限設置得很小。
一般來說,渦街流量計在小流量時(低頻處)頻率計算結果波動比較大,而大流量時(高頻處)比較穩定。所以,門限值可以根據渦街流量計所能測的最低頻率來設置。由于流量計的最高可測頻率是已知的,而采樣頻率一般設為略大于最高頻率的2倍,所以,門限值可以根據式(1)來計算:
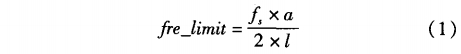
式中:ƒs為采樣頻率;Ɩ為儀表量程比;α(0<lαl<1)為系數。調整α可以調整門限值大小,α<0時為下限;α>0時為上限。一般可以取±4%~±13%。
當流量突變不超過門限時,在流量計調節時間內累積流量的最大相對誤差為:
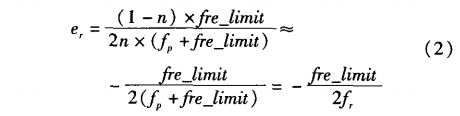
式中:n(n》1)為平均次數;ƒp為突變以前的頻率;ƒr為突變以后的頻率。而當流量突變超過fre_limit時,誤差會非常小。
實際流量變化是一個連續變化的過程。但是,只要流量對應的信號頻率的變化率超過fre_limit/tc,其中tc為FFT計算的間隔時間,則系統就能快速響應;而流量對應的信號頻率的變化率小于fre_limit/tc.時,其最大相對誤差小于式(2)的計算值。
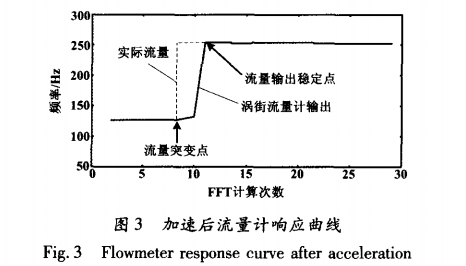
圖3為經過加速處理后40口徑渦街流量計在流量突變時的響應曲線。可見,在流量突變后,系統經過3次FFT計算就能跟上流量的變化,有效地提高了流量計的響應速度。
2.1消除輸出信號的斷續現象
頻譜分析法是按能量最大原則,即把FFT計算出來的功率譜中能量最大的頻率值作為渦街頻率。但是,由于干擾的存在,不得不設置一個最小截止幅值(min_amp)來限制小幅值干擾信號,即當FFT計算幅值低于最小截止幅值時,流量計輸出為0,從而提高抗干擾能力;而由于信號質量、對采樣信號加窗FFT非整周期采樣等原因,導致FFT計算幅值會有波動。當流量在流量計下限附近時,會出現FFT計算幅值低于最小截止幅值的情況,這將導致流量計輸出出現斷續現象。
流量計斷續問題主要是由于偶爾幾次的FFT計算幅值低于最小截止幅值所致。通過實驗發現,在流量計可測流量范圍內-般不會出現連續幾次FFT計算幅值均小于最小截止幅值的情況,所以在碰到FFT計算幅值低于最小截止幅值時不是直接輸出0,而是將0放入隊列Q1。在計算平均頻率以前先對隊列Q1中最近的N(N可取3~4)個值進行判斷,如果N個值,全部為0,則流量計輸出為0,否則繼續做平均計算,將平均值作為流量計的輸出頻率,這樣就可以解決輸出斷續的問題。
2.2解決輸出信號的波動問題
在小流量的時候渦街流量計信號微弱,信噪比降低,信號質量比較差,頻譜分析得到的渦街頻率波動比較大。特別是小口徑渦街流量計,由于傳感器安裝等原因,這種現象更為明顯。圖4中,曲線1為15口徑渦街流量計在下限頻率附近,每次FFT計算得到的渦街頻率;曲線2為40口徑離下限頻率比較遠時每次FFT計算后得到的渦街頻率。可見,曲線1波動較大,數值約為30Hz。此時,即便采取平均措施,也無法使輸出頻率值穩定。
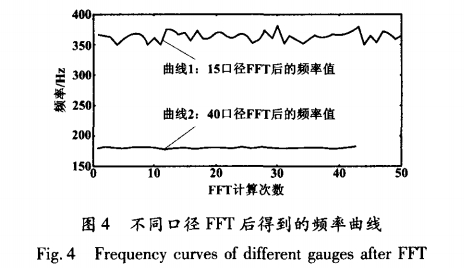
波動問題主要是由于信號較差,每次FFT計算出的頻率值偏差太大所造成的。所以,首先必須保證隊列Q1中的所有頻率值在可信范圍內,即在流量沒有突變的情況下,隊列Q1中的頻率值不能與前次輸出頻率差得太多。為此,可以設置一個頻率允許跳動范圍的限幅值。當計算的頻率值超出范圍時,不是簡單地將這個值去掉,而是用最近一次的輸出頻率加上限幅值來代替這個值。這在某種程度上能保留反映流量變化趨勢的部分信息。通過實驗發現,可以根據fre__limit來設置這個限幅值。
處理波動問題的具體步驟為:
①對隊列Q,的第N個元素Q1[N]用式(3)處理,得到數值ƒin為:
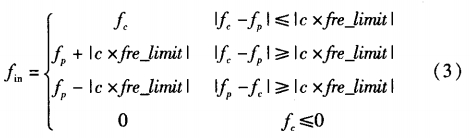
式中:ƒin為處理后隊列Q1[N]中的頻率值;f。為處理前隊列Q1N]中的頻率值,即原先FFT計算出來的頻率值;f,為流量計最近--次輸出的頻率值;c為常數,可以根據實際情況選取,實驗中取1。需要注意的是,這里是對Q1[N]處理,而不是對隊首元素Q1[1]處理。原因是,Q1[1]~Q1[N-1]中的信息會反映流量的突變,如果對其進行限幅處理,會影響系統的響應速度。
②對隊列Q1中的值進行去N-1次最大、最小值處理,算出均值μ,根據均值算出標準差σ,然后,再利用標準差對隊列Q1中的值進行平均。而超出標準差的數據不參加平均。
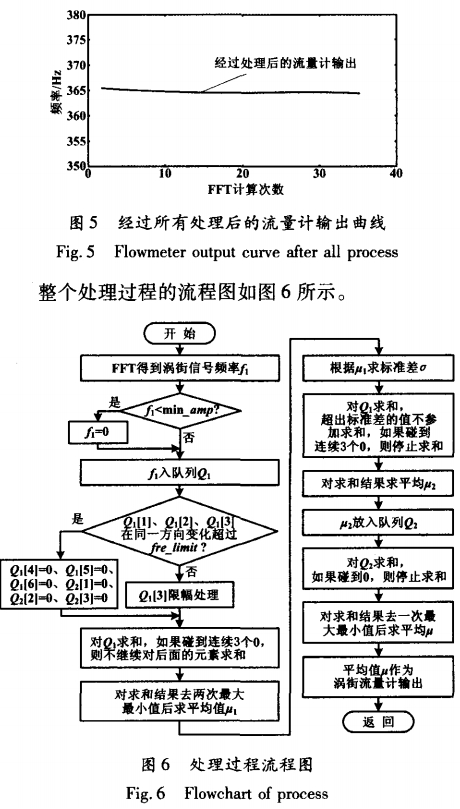
③經過以上處理后得到的頻率已經比較穩定,但仍有一定范圍的波動。如果流量是穩定的話,流量計輸出應該接近穩定,波動比較小。因此,可以考慮對計算頻率值進行第二次平均,相當于進行二次濾波。為此,建立另一個隊列Q2。隊列Q2中的元素是隊列Q;經過上述步驟處理后的結果;再對隊列Q2進行平均計算,得到的均值作為流量計的輸出。注意,這里對隊列Q2也要進行加速處理,方法與處理Q1的類似。圖5所示為經過處理以后渦街流量計的輸出,從圖中可以看出流量計輸出已經比較平穩。
3結束語
根據頻譜分析后的結果,采用設置門限值的方法對流量計輸出進行加速處理,并分析了加速處理方法的誤差,有效地提高了流量計的響應速度降低了調節時間內由于響應慢造成的誤差。
對頻譜分析后的結果進行0值判斷,連續幾次為0,流量計輸出才為0,消除了流量計在可測流量下限.時輸出斷續現象。
在對頻譜分析后的結果平均前采取了限幅、去掉超過標準差以外的值和去掉最大值最小值的操作,并對平均后的結果進行第二次平均,減小了流量計輸出信號的波動,提高了流量計輸出的穩定性。
文章來源于網絡,如有侵權聯系即刪除!